solving quadratic equations by factoring worksheet pdf

Quadratic equations, involving squared terms, are fundamental in mathematics. They describe relationships where a quantity is squared,
appearing in diverse applications like projectile motion and area calculations. Mastering these equations unlocks problem-solving capabilities.

What is a Quadratic Equation?

A quadratic equation is a polynomial equation of the second degree. This means the highest power of the variable in the equation is 2. Generally, these equations explore relationships involving squares, stemming from the Latin word “quadratus” meaning square. They are crucial in modeling various real-world scenarios, from the trajectory of a projectile to calculating areas.

Mathematically, a quadratic equation isn’t simply about squaring; it encompasses terms where the variable is raised to the power of two. Understanding this foundational concept is vital before delving into solution techniques like factoring, which is a method to rewrite the equation as a product of simpler expressions. The ability to identify and manipulate these equations is a cornerstone of algebraic proficiency, frequently tested in exams like the IBPS RRB.

These equations are often used to represent parabolic curves, and their solutions, known as roots, represent the points where the parabola intersects the x-axis.

The Standard Form of a Quadratic Equation

The standard form of a quadratic equation is expressed as ax² + bx + c = 0, where ‘a’, ‘b’, and ‘c’ are constants, and ‘a’ is not equal to zero. This standardized representation is crucial for applying various solution methods, including factoring, and for consistently interpreting the equation’s components.

The coefficients ‘a’, ‘b’, and ‘c’ dictate the parabola’s shape and position on a coordinate plane. ‘a’ influences the parabola’s width and direction (opening upwards if positive, downwards if negative). ‘b’ affects the parabola’s axis of symmetry, and ‘c’ represents the y-intercept – the point where the parabola crosses the y-axis.

Recognizing this standard form is the first step in solving quadratic equations. It allows for a systematic approach, whether employing factoring, the quadratic formula, or completing the square. Competency-based assessments, like those in CBSE exams, often require students to identify and manipulate equations in this standard form.

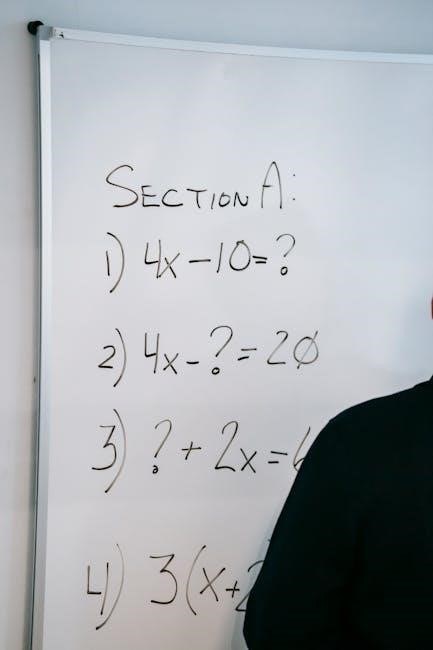
Solving Quadratic Equations by Factoring

Factoring is a technique to rewrite a quadratic equation as a product of linear expressions. This method relies on finding two numbers that satisfy specific conditions, simplifying solutions.

Understanding the Zero Product Property

The Zero Product Property is a cornerstone principle in solving quadratic equations by factoring. It states that if the product of two or more factors is zero, then at least one of the factors must be zero. Mathematically, this is expressed as: if a * b = 0, then a = 0 or b = 0 (or both).

This property is crucial because factoring transforms a quadratic equation into a form where one side is a product of linear factors set equal to zero. For example, if we have (x ⎼ 2)(x + 3) = 0, the Zero Product Property allows us to conclude that either (x ⎼ 2) = 0 or (x + 3) = 0.

Solving each of these linear equations individually then yields the solutions to the original quadratic equation. In this case, x = 2 or x = -3. Understanding this property is fundamental to successfully applying the factoring method and finding all possible solutions to quadratic equations. It’s a powerful tool for simplifying complex problems.

Steps for Solving by Factoring

Solving quadratic equations by factoring involves a systematic approach. First, rewrite the equation in standard form: ax² + bx + c = 0. Next, factor the quadratic expression on the left side into two linear factors; This step often requires finding two numbers that multiply to ‘ac’ and add up to ‘b’.

Once factored, apply the Zero Product Property. Set each factor equal to zero and solve the resulting linear equations. These solutions represent the roots or x-intercepts of the quadratic equation. It’s crucial to check your solutions by substituting them back into the original equation to ensure they satisfy the equation.

Remember to look for a greatest common factor (GCF) before attempting to factor. Factoring out the GCF simplifies the equation and can make the subsequent steps easier. Practice is key to mastering this technique, and worksheets provide valuable opportunities to hone your skills.

Example 1: Simple Factoring

Let’s consider the equation: x² + 5x + 6 = 0. Our goal is to factor the quadratic expression. We need two numbers that multiply to 6 and add to 5. Those numbers are 2 and 3.

Therefore, we can rewrite the equation as (x + 2)(x + 3) = 0. Now, applying the Zero Product Property, we set each factor equal to zero:

x + 2 = 0 or x + 3 = 0

Solving for x in each equation, we get:

x = -2 or x = -3

Thus, the solutions to the equation x² + 5x + 6 = 0 are x = -2 and x = -3. Always verify these solutions by substituting them back into the original equation to confirm their validity. This simple example demonstrates the core principle of factoring to solve quadratic equations, a skill reinforced through practice with worksheets.

Example 2: Factoring with a Leading Coefficient

Consider the equation: 2x² + 7x + 3 = 0. This presents a slightly greater challenge due to the leading coefficient of 2. We need to find two numbers that multiply to (2 * 3) = 6 and add to 7. Those numbers are 6 and 1.

We rewrite the middle term using these numbers: 2x² + 6x + x + 3 = 0. Now, we factor by grouping:

2x(x + 3) + 1(x + 3) = 0

Notice that (x + 3) is a common factor. Factoring it out, we get:

(2x + 1)(x + 3) = 0

Applying the Zero Product Property:

2x + 1 = 0 or x + 3 = 0

Solving for x:

x = -1/2 or x = -3

Therefore, the solutions are x = -1/2 and x = -3. This example illustrates a common technique for factoring quadratics with a leading coefficient, a skill honed through dedicated practice using factoring worksheets.

Quadratic Equations in Real-World Applications

Real-world scenarios frequently utilize quadratic equations, modeling phenomena like projectile trajectories and area calculations. Solving these equations, often via factoring, provides practical insights and solutions.

Modeling Projectile Motion

Projectile motion, the path an object takes when thrown or launched, is beautifully described by quadratic equations. Ignoring air resistance, the vertical position of a projectile over time can be modeled using the equation h(t) = -16t² + v₀t + h₀, where ‘h(t)’ represents the height at time ‘t’, ‘v₀’ is the initial vertical velocity, and ‘h₀’ is the initial height.

Understanding this equation allows us to determine crucial information, such as the maximum height reached by the projectile, the time it takes to hit the ground, and its range. Solving for ‘t’ when h(t) = 0 (ground level) often involves factoring the quadratic equation. This process helps pinpoint the projectile’s flight duration.

For instance, if a ball is thrown upwards from a height of 5 feet with an initial velocity of 30 feet per second, the equation becomes h(t) = -16t² + 30t + 5. Factoring (or using the quadratic formula) allows us to find the times when the ball returns to the ground, demonstrating the practical application of quadratic equations in physics and engineering.

Area Calculation Problems

Quadratic equations frequently arise when calculating areas of geometric shapes, particularly those involving changes in dimensions or composite figures. Consider a rectangular garden whose length is 3 meters more than its width. If the area of the garden is 70 square meters, we can represent this situation with a quadratic equation.

Let ‘w’ represent the width. Then the length is ‘w + 3’. The area is given by length times width: w(w + 3) = 70. Expanding this gives w² + 3w = 70, which rearranges to w² + 3w ⎼ 70 = 0. Solving this quadratic equation by factoring (or other methods) allows us to determine the width of the garden.

Similarly, problems involving areas of combined shapes, where one shape is embedded within another, often lead to quadratic equations. Finding the dimensions of the surrounding shape, given the area of the inner shape and some relationship between their sides, requires solving these equations. These applications highlight the practical relevance of quadratic equations in geometry and real-world design.

Worksheet Resources & Practice

Numerous online resources offer free, printable PDF worksheets for practicing quadratic equation factoring. These worksheets provide varied problems, aiding skill development and reinforcing concepts effectively.

Finding Free Printable PDF Worksheets

Locating high-quality, free printable PDF worksheets for solving quadratic equations by factoring is surprisingly accessible. A quick online search using keywords like “quadratic equations factoring worksheet PDF” yields a wealth of options. Websites dedicated to mathematics education, such as Khan Academy, offer comprehensive resources, including practice exercises with answer keys.

Many educational websites provide worksheets categorized by difficulty level, allowing students to progress at their own pace. Platforms like Math-Drills.com and Kuta Software also host extensive collections of printable worksheets covering various algebraic topics, including quadratic equations. These resources often include worksheets with varying levels of complexity, from simple factoring problems to more challenging scenarios involving leading coefficients and special cases.

Furthermore, teachers and educators frequently share their created worksheets online, contributing to a diverse pool of available materials. Always preview the worksheet to ensure it aligns with the specific factoring techniques being taught and to verify the accuracy of the answer key. Utilizing these readily available resources can significantly enhance practice and understanding.

Types of Problems Included in Worksheets

Quadratic factoring worksheets typically begin with straightforward problems, asking students to solve equations where the leading coefficient is 1. These build foundational skills. As difficulty increases, worksheets introduce equations with a leading coefficient greater than 1, requiring more complex factoring techniques like grouping or trial and error.

Common problem types include finding the roots (or zeros) of a quadratic equation, determining the solutions that satisfy the equation, and applying the zero product property. Worksheets also frequently present equations in various forms – standard form, factored form, and sometimes requiring students to convert between forms before factoring.

More advanced worksheets incorporate word problems that require students to translate real-world scenarios into quadratic equations and then solve them by factoring. These problems test not only factoring skills but also problem-solving and analytical abilities. Some worksheets also include problems where students need to check their solutions to ensure they are valid.

Answer Keys and Solutions

Comprehensive answer keys are crucial components of solving quadratic equations by factoring worksheets. These keys typically provide not just the final answers (the roots of the equation), but also detailed, step-by-step solutions demonstrating the factoring process. This allows students to understand how to arrive at the correct answer, not just what the answer is.

Detailed solutions often show the initial factoring setup, the identification of factors, the application of the zero product property, and the final determination of the solutions. Some answer keys may offer multiple solution paths, acknowledging that there can be different valid ways to factor a quadratic expression.

High-quality resources also include explanations for any potential pitfalls or common errors students might encounter, helping them avoid these mistakes in the future. Furthermore, some keys provide checks for extraneous solutions, ensuring the validity of the answers within the original equation’s context.

Advanced Topics & Considerations

Beyond factoring, the quadratic formula offers a universal solution. When factoring proves difficult or impossible, this formula reliably finds roots, expanding problem-solving skills.

Quadratic Formula as an Alternative Method

While factoring is an elegant approach, not all quadratic equations readily succumb to this technique. This is where the quadratic formula emerges as a powerful and universally applicable alternative. Derived from completing the square, the formula provides a direct path to finding the roots of any quadratic equation, regardless of its complexity.

The quadratic formula is expressed as: x = (-b ± √(b² ౼ 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation in its standard form (ax² + bx + c = 0). The expression within the square root, b² ⎼ 4ac, is known as the discriminant. It reveals the nature of the roots – whether they are real and distinct, real and equal, or complex.

Employing the quadratic formula guarantees a solution, even when factoring feels intractable. It’s a crucial tool for students to master, ensuring they can confidently tackle any quadratic equation presented to them, especially when worksheets present challenging scenarios where factoring isn’t straightforward. This method provides a reliable backup and reinforces understanding of quadratic equation properties.

When Factoring is Not Possible

Despite its efficiency, factoring isn’t always a viable solution for quadratic equations. Certain equations simply don’t factor neatly into rational expressions. This often occurs when the roots are irrational numbers – those that cannot be expressed as simple fractions – or complex numbers, involving the imaginary unit ‘i’.

For instance, equations like x² + x + 1 = 0 or 2x² ⎼ 4x + 5 = 0 resist straightforward factoring. Attempting to find two numbers that multiply to the constant term and add up to the coefficient of the linear term proves fruitless in these cases. This is where alternative methods, such as the quadratic formula or completing the square, become essential.

Worksheets focusing on quadratic equations often include such examples to challenge students and encourage them to explore diverse solution techniques. Recognizing when factoring is impractical is a crucial skill, preventing wasted effort and promoting a more comprehensive understanding of quadratic equation solving. It highlights the importance of having multiple tools at one’s disposal.