solving two-step equations word problems worksheet pdf with answers

Two-step equations word problems involve real-world scenarios requiring algebraic solutions. Worksheets with PDF formats and answer keys provide structured practice, helping students master these essential math skills effectively.

1.1 What Are Two-Step Equations?

Two-step equations are algebraic expressions requiring two operations to solve. They often involve combining numbers and then multiplying or dividing. For example, solving (2x + 3 = 7) involves subtracting 3 and then dividing by 2. These equations are fundamental in math education, as they build problem-solving skills. Worksheets with two-step equations, especially in PDF format, provide structured practice. They include word problems that mirror real-life scenarios, helping students apply mathematical concepts to practical situations. Answer keys are often included for self-assessment and accuracy checks.

1.2 Importance of Word Problems in Math Education

Word problems are essential in math education as they bridge abstract concepts and real-world applications. They enhance critical thinking and problem-solving skills by requiring students to interpret and translate scenarios into mathematical expressions. Two-step equation word problems, in particular, help students develop logical reasoning and algebraic manipulation. Worksheets with answer keys provide immediate feedback, fostering self-assessment and understanding. These resources are invaluable for building confidence and fluency in solving practical math challenges, preparing students for higher-level mathematics and everyday problem-solving tasks.

Understanding the Structure of Two-Step Equations

Two-step equations involve combining operations like addition and multiplication. They require identifying operations and isolating the variable in two distinct steps, forming a clear problem-solving structure.

2.1 Identifying Operations in Equations

Identifying operations in two-step equations is crucial for solving word problems. These equations often involve combinations of addition, subtraction, multiplication, or division. Recognizing the sequence of operations helps in setting up the equation correctly. For example, understanding whether multiplication precedes addition or vice versa is essential. Worksheets with answer keys provide clear examples, allowing students to practice identifying and applying these operations accurately. This skill is foundational for translating word problems into mathematical expressions and solving them effectively.

2.2 Setting Up Equations from Word Problems

Setting up equations from word problems involves translating words into mathematical expressions. Identify key details, such as unknowns and operations, to form a two-step equation. For example, “A number increased by 5 and then doubled” becomes 2(x + 5). Worksheets with answer keys guide students in practicing this translation, ensuring equations are set up correctly. PDF resources provide structured problems, helping students master the skill of converting real-world scenarios into solvable algebraic equations with clarity and precision.

Solving Two-Step Equations

Solving two-step equations involves isolating the variable by reversing operations in the correct order. Divide by coefficients and check solutions by substituting back into the original problem.

3.1 Step-by-Step Approach to Solving

To solve two-step equations, start by identifying the operations applied to the variable. Reverse these operations in the opposite order, first undoing addition or subtraction, then multiplication or division. For example, in the equation (2x + 3 = 7), subtract 3 from both sides before dividing by 2. Always check your solution by substituting it back into the original equation to ensure equality. This methodical approach ensures accuracy and builds confidence in solving word problems effectively.

3.2 Checking Solutions for Accuracy

After solving a two-step equation, substitute the solution back into the original problem to verify accuracy. This ensures both sides of the equation are equal. For instance, if x = 4 solves 2x + 3 = 11, substituting gives 2(4) + 3 = 11, confirming the solution. Using answer keys from worksheets provides immediate feedback, helping identify errors. Regularly checking solutions reinforces problem-solving skills and builds confidence in tackling word problems effectively. This step is crucial for mastering two-step equations and ensuring mathematical accuracy.

Benefits of Using Worksheets for Practice

Worksheets provide structured practice, enhancing problem-solving skills. PDF formats offer convenience, while answer keys enable self-assessment, fostering independence and confidence in mastering two-step equations and word problems effectively.

4.1 Advantages of PDF Format

PDF formats offer portability and accessibility, allowing worksheets to be viewed on any device. They are easily printable, maintaining clarity and structure. PDFs also enable the inclusion of answer keys, facilitating self-assessment. This format ensures consistency and readability, making it ideal for distributing practice materials. Worksheets in PDF are widely compatible and require no special software, enhancing their usability. They provide a reliable resource for students to practice two-step equations and word problems, supporting structured learning and skill mastery effectively.

4.2 Role of Answer Keys in Learning

Answer keys play a vital role in the learning process by providing immediate feedback and verification of solutions. They enable students to self-assess their work, identify errors, and understand correct methods. Including answer keys in worksheets ensures accountability and reinforces understanding. Teachers and learners alike benefit from this feature, as it saves time and promotes independent practice. The availability of answer keys in PDF formats enhances accessibility, making them a valuable resource for both in-class and homework assignments, fostering a deeper grasp of two-step equations and word problems.

Differentiating Instruction with Worksheets

Worksheets offer varied problems to suit different learning levels, helping teachers cater to individual student needs and abilities effectively in the classroom setting.

5.1 Catering to Various Learning Levels

Worksheets are designed to accommodate students at different learning stages, offering problems that range from basic to advanced. For instance, Worksheet Version A provides 12 easier problems, while others include more complex scenarios. These resources are suitable for 6th to 8th-grade students, ensuring each learner can find challenges that match their skill level. The inclusion of both number and word problems, involving integers, fractions, and decimals, allows for a gradual progression. This differentiation helps teachers address diverse classroom needs effectively, ensuring all students can grow confidently in their problem-solving abilities.

5.2 Customizing Problems for Different Grades

Worksheets are tailored to meet the needs of specific grade levels, ensuring problems align with curriculum standards. For example, 7th-grade worksheets focus on CCSS.7.EE.B.4.A, while 8th-grade problems incorporate more complex numbers. The difficulty of equations and word problems is adjusted to suit younger or older students, with simpler integers for 6th graders and decimals for advanced learners. This customization ensures that each grade level receives appropriate challenges, fostering skill development and confidence in solving two-step equations.

Worksheet Design and Components

Worksheets feature clear layouts with readable fonts, organized problem sets, and answer keys. They include a mix of number and word problems, ensuring varied practice opportunities for students.

6.1 Types of Problems Included

Worksheets include a variety of problems such as number and word problems, geometric shapes, and real-world scenarios. They cover integers, fractions, and decimals, catering to different learning levels and grades. Problems are designed to require two-step operations, ensuring focused practice on specific skills. Word problems often involve interpreting contexts like field trips or resource distribution, making math relevant and engaging. Mixed problem types help students apply algebraic concepts to diverse situations, reinforcing their understanding and problem-solving abilities effectively.

6.2 Layout and Readability Features

Worksheets are designed with clear formatting and spacing to enhance readability. Problems are presented in a structured manner, with clean fonts and organized layouts. PDF formats ensure consistency across devices, making them easy to print or view digitally. Answer keys are often included at the end, allowing students to self-assess without confusion. The design minimizes visual clutter, focusing attention on the problems and solutions. This user-friendly approach helps students concentrate on learning and practicing two-step equations effectively.

Interpreting Word Problems

Interpreting word problems involves translating real-world scenarios into mathematical expressions. Worksheets guide students in identifying key details and setting up equations to solve two-step problems effectively.

7.1 Translating Words into Mathematical Expressions

Translating words into mathematical expressions is a critical skill for solving two-step equations. Worksheets guide students in identifying key terms like “divided into” or “twice as many,” which translate into division or multiplication. For example, “A number divided by 4 equals 6” becomes ( rac{x}{4} = 6 ). Students learn to underline important words and convert phrases into operations, ensuring accurate equation setup. This step enhances problem-solving skills and understanding of algebraic structures, making it easier to apply inverse operations for solutions.

7.2 Identifying Key Information in Problems

Identifying key information in word problems is essential for setting up accurate equations. Students learn to underline or highlight important details such as numbers, operations, and relationships. For example, in “331 students went on a field trip. Six buses were filled and 7 students traveled in cars,” the numbers 331, 6, and 7 are crucial. Understanding the context helps determine whether to add, subtract, multiply, or divide. This skill enables students to focus on relevant data, ensuring their equations align with the problem’s requirements and lead to correct solutions.

Setting Up and Solving Equations

Setting up equations involves translating word problems into mathematical expressions. Solving requires applying inverse operations in the correct order, ensuring accuracy and verifying solutions by substitution.

8.1 Writing Equations from Word Problems

Writing equations from word problems involves identifying key information and translating it into mathematical expressions. For example, in a problem like “331 students went on a field trip, with 6 buses filled and 7 students in cars,” students assign variables and set up equations to represent the scenario. This process enhances problem-solving skills and understanding of real-world applications. Worksheets in PDF format provide structured practice, while answer keys allow for self-assessment and verification of solutions.

8.2 Solving Equations with Multiple Steps

Solving two-step equations requires a systematic approach. First, identify and perform the inverse operation to isolate the variable. For example, in the equation (2x + 3 = 11), subtract 3 from both sides, then divide by 2. Always check solutions by substituting them back into the original equation to ensure equality. Worksheets with answer keys provide practice opportunities, helping students master these skills and build confidence in solving real-world problems effectively.

Checking Solutions

Substitute solutions back into original equations to verify equality. Answer keys provide correct answers, ensuring accuracy and helping students identify mistakes in their problem-solving process.

9.1 Substituting Solutions Back into Original Problems

Substituting solutions back into original problems ensures accuracy. By replacing the variable with the found value, students verify if both sides of the equation are equal. This step confirms correctness and reinforces understanding. Answer keys provide correct solutions, allowing self-assessment and identification of common mistakes. Regular practice with worksheets helps build confidence and fluency in solving two-step equations. This methodical approach ensures students grasp the practical application of algebraic concepts in real-world scenarios, making learning both effective and engaging.

9.2 Verifying Equality on Both Sides

Verifying equality ensures both sides of the equation balance after substitution. For example, substituting ( x = 4 ) into ( 2x + 3 = 11 ) results in ( 2(4) + 3 = 11 ), simplifying to ( 11 = 11 ). This confirmation proves the solution’s accuracy. Answer keys provide correct solutions, enabling students to check their work and identify errors. Regular practice with worksheets reinforces this critical step, ensuring students develop a strong foundation in solving two-step equations and understanding the importance of verification in mathematical problem-solving.

Answer Keys and Their Role

Answer keys provide correct solutions, enabling students to verify their work and identify mistakes. They serve as essential tools for self-assessment and reinforce learning effectively.

10.1 Importance of Answer Keys for Self-Assessment

Answer keys are vital for self-assessment, allowing students to verify their solutions and identify errors. They provide immediate feedback, helping learners understand their progress and strengthen problem-solving skills. By comparing their answers with the correct solutions, students can pinpoint mistakes and improve their understanding of two-step equations. This self-assessment tool fosters independence and confidence, enabling learners to master word problems effectively. Answer keys also serve as a resource for teachers to track student performance and address common misconceptions in the classroom.

10.2 Using Answer Keys to Identify Common Mistakes

Answer keys are invaluable for identifying common mistakes in solving two-step equations. By comparing their solutions to the correct answers, students can pinpoint errors in their problem-solving process. For instance, many students struggle with reversing operations or misapplying mathematical properties. Answer keys highlight these frequent pitfalls, enabling learners to address specific weaknesses. Teachers can also use answer keys to identify widespread misconceptions in the classroom, tailoring instruction to address these areas. This targeted feedback enhances learning and improves overall mastery of two-step equations.

Additional Resources and Practice Materials

Supplement your learning with free PDF worksheets from Kuta Software and ByteLearn.com. These resources offer printable two-step equation word problems with answer keys, ideal for all grade levels.

11.1 Recommended Websites for Worksheets

For high-quality two-step equation word problem worksheets, visit Kuta Software and ByteLearn.com. These websites offer free, downloadable PDF resources with answer keys. Kuta Software provides a variety of worksheets, including “Two-Step Equation Word Problems,” suitable for different grade levels. ByteLearn.com offers worksheets aligned with Common Core standards, ensuring educational relevance. Both sites cater to diverse learning needs, with problems involving integers, fractions, and real-world scenarios. These resources are ideal for teachers and students seeking comprehensive practice materials.

11.2 Supplementary Activities for Reinforcement

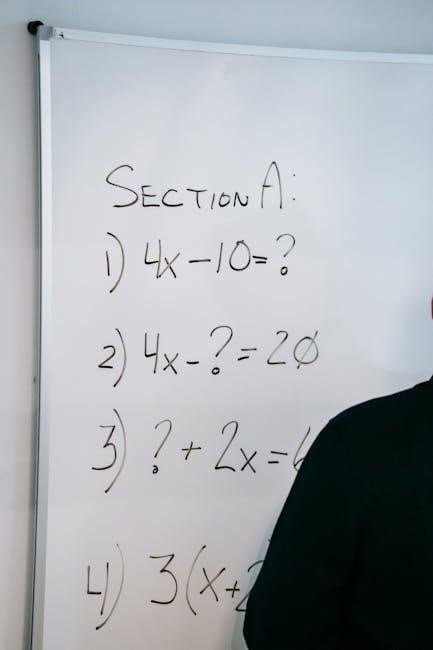
Beyond worksheets, interactive tools like online quizzes and educational apps can enhance learning. Real-world application activities, such as calculating expenses or measuring materials, make equations relatable. Collaborative projects, where students create and solve problems in groups, foster teamwork and understanding. These activities reinforce problem-solving skills and deepen mathematical comprehension, ensuring a well-rounded grasp of two-step equations.

Conclusion

Mastering two-step equations through practice worksheets and answer keys enhances problem-solving skills, builds confidence, and prepares students for real-world math challenges. Consistent practice ensures long-term understanding and success.

12.1 Summary of Key Points

Two-step equations word problems are essential for developing algebraic thinking and real-world problem-solving skills. Worksheets in PDF format, often accompanied by answer keys, provide structured practice. These resources cater to various learning levels, ensuring differentiation for diverse student needs. Regular practice with such materials enhances understanding, boosts confidence, and reinforces mathematical concepts. Answer keys enable self-assessment, helping students identify mistakes and improve accuracy. Consistent use of these worksheets fosters mastery of two-step equations, preparing learners for more complex math challenges ahead.

12.2 Encouragement for Continued Practice

Consistent practice with two-step equations word problems is crucial for mastery. Utilize PDF worksheets with answer keys to reinforce learning and build confidence. Regularly tackling these problems enhances problem-solving skills and prepares students for more complex math. Encourage learners to explore additional resources and activities for varied practice. Celebrate progress, no matter how small, to maintain motivation. With dedication and persistence, students will become proficient in solving two-step equations, unlocking their full potential in mathematics.